GDC 2002: Dynamic Level of Detail Terrain Rendering with Bézier Patches 

This paper discusses the terrain system used in SSX. An algorithm for the tessellation of polynomial surfaces is presented. The system allows for adaptive tessellation with continuous level-of-detail while avoiding the introduction of cracks and seams between adjacent surfaces with different geometric resolution. The Surface lighting on the terrain is discussed.

Introduction

A high order parametric surface representation is chosen for representing the terrain in the SSX snowboarding game. The reasoning behind this decision is to represent the snow surface with an elegant and concise mathematical representation for physics calculations, and to allow for an arbitrary polygonal resolution for rendering the terrain while insuring a small memory footprint for the surface information.

Bézier patches are chosen for their fast run time evaluation, affine invariance, and convex hull property (for quick occlusion and intersection tests). The terrain is represented as a grid of Bi-cubic Bézier surfaces.

Each Bi-cubic Bézier surface or patch is defined by a set of control points. From these control points we can generate any point on the surface. We tessellate the patch by connecting a grid of evaluated surface points into triangles or triangle strips. The polygon primitives can then be rendered by conventional 3D hardware. We can tessellate the patch to an arbitrary resolution at run time. In order to achieve a high quality image with reasonable performance it is desirable to evaluate the patches at different resolutions. A heuristic is required for determining what resolution a patch should be evaluated at. For this implementation a simple distance based Level of Detail heuristic is used. Evaluating neighbouring patches at different LOD will introduce ugly gaps in the rendered surface. Special transition patches are generated to solve this problem.

Traditional polygonal lighting models require a vertex-normal pair in order to generate a colour for each vertex. The graphics hardware interpolates the vertex colours over the polygon surface. With dynamic evaluation of a parametric surface the number of vertices and their position will be changing. As a result a dynamically tessellated vertex-normal lighting system will tend to pop and move which will detract from the quality of the moving image. In order to avoid this one must decouple the geometric resolution from the light sample resolution. We use light-maps. Light maps encode lighting as 2D textures. At run time the light map texture is modulated with a surface texture of each polygon to create the final image. With this method the surface lighting does not pop when the geometric resolution changes. We also have the added benefit of calculating the lighting off-line using whatever lighting model we like. The trade off is we lose the ability to dynamically change the surface lighting without recalculating light maps at run time.

Background

A parametric curve defined in three dimensions is given by three univariate functions:

     

As u varies from 0 to 1 the functions sweep out the curve. Similarly a parametric surface is defined by three bivariate functions:

As we vary u from 0 to 1 and we hold v constant we sweep out a curve in three-space. An infinity of such curves exists as we vary v from 0 to 1 and this defines the surface in three dimensions.

A Parametric curve is usually a polynomial:

Computer graphics generally stick to a degree of 3 that is cubic. For degrees greater then 3 there is a trade off between curve flexibility and descriptions that are more cumbersome to work with. The cubic form looks like this:

The relationship between the shape of the curve and the coefficients p_i are not very intuitive. Instead of having to manipulate the coefficients directly, the polynomial form can be rearranged into control points and basis functions, which provide a more intuitive connection to the shape of the curve:

     

The co-ordinates p_i are called control points and the power basis is b_i(u). The cubic basis is a collection of linearly independent polynomial b_i(u) given by:

For equation 2 the control points are (p⁰, p¹, p², and p³) and the basis polynomial are (1, u, u² and u³).

A bi-cubic parametric surface has the form of equation 3 and is traced out as the parameters (u,v) take all possible values between 0 and 1. This is known as a patch. Free form surfaces are modelled using nets of patches. Bi-cubic parametric patches are defined over a rectangular domain in uv-space and the boundary curves of the patch are themselves cubic polynomial curves. A point Q with the co-ordinates (x,y,z) in Cartesian space is represented by the parameters (u,v) in parametric space. Using the same control point and basis function representation we define the patch as:

Where p_ij is a set of 16 control points:

p₀₀ p₀₁ p₀₂ p₀₃
p₁₀ p₁₁ p₁₂ p₁₃
p₂₀ p₂₁ p₂₂ p₂₃
p₃₀ p₃₁ p₃₂ p₃₃

The net of control points forms a polyhedron in Cartesian space and the position of the points in this space controls the shape of the surface.

The basis used for rendering the patches in SSX is the Bézier basis. The Bézier basis polynomial are called Bernstein polynomials and are defined by:

where:

For a cubic Bézier curve the basis functions are:

These curves show the influence that each control point has on the final curve form.
When u=0 the basis function B_0,3 = 1 while the others are 0. When u=1 the basis function B_3,3 = 1 while the others are 0. From this we know that when u=0, p₀ will have the most influence and when u=1, p₃ will have the most influence. The control points p₁ and p₂ have the most effect when u=1/3 and u=2/3 respectively. The manner in which the basis functions affect the shape of the curve is the reason they are called blending functions. An alternate convention for specifying a Bézier curve is the matrix convention:

The Bézier patch is defined in matrix notation by:

This matrix form is what is used in SSX. Figure 1 shows the control net P_c of 16 control points that is needed to describe a single patch. The transpose of Bézier matrix M_B^T has the same form as M_B. If we assume that the control matrix P_C does not change then we can pre-multiply these to get:

Figure 1: Control polyhedron (left) and resulting bi-cubic Bézier patch (right)

Level of Detail System

To create an image that most accurately represents the terrain surface as described by the artist we want to evaluate the curved surfaces to a high level of detail. If all patches are tessellated to the same degree then we will generate just as much polygonal detail for far away patches as we do for close up patches. The total number of polygons that the hardware is required to render in most cases will limit us to a lower geometric resolution than we would like. With an LOD system we render polygon detail only where it is required. The results are near identical quality with fewer polygons to render. Unfortunately if all patches are not evaluated to the same degree, seams and "tearing" will be seen between the patches. The result is quite unacceptable for the quality expected of modern video games. The goal is to tessellate patches to different degrees without generating seems.

The algorithm presented here ensures that no tears or seams are created between neighbouring patches with different tessellation levels. The only constraint is that patches must have at least C⁰ continuity with their neighbours. C⁰ continuity requires that neighbouring patches share control points along the boundary connecting them. Note that C¹ continuity is required for smooth lighting and physics calculations between patches but is not required for the LOD algorithm to work.

With these constraints in place the run time evaluation of the terrain will not need to be aware of neighbouring information to produce a seamless tessellation of the entire terrain with changing LOD. Most other algorithms that fix the "cracking" problem require neighbour information and usually a second pass in order to correct errors. The evaluation of the Bézier polynomial can be performed using various methods depending on the implementer's preference. There are many methods of evaluating equation 4 such as direct evaluation, forward differencing, and recursive subdivision. The evaluation method chosen to implement this system is not important.

A run time heuristic is used to determine the tessellation level of each of the four boundary curves of the Bézier patch. If each boundary curve requires the same level, then the entire patch is uniformly tessellated to the same degree. If the 4 boundary levels differ, then a non-uniform patch is generated. The number of edge vertices generated is directly a function of the boundary edge heuristic. As such the number of vertices on the boundary of two patches is always the same so long as C⁰ edge continuity exists. The "cracking" problem is reduced to ensuring that a non-uniform patch does not create any inner cracks or seems while retaining the number of edge vertices as determined by the boundary heuristic.

A non-uniform patch is treated as a uniform inner patch connected to the edge vertices with 4 triangle strips. Let the number of points per edge be specified clockwise as E0, E1, E2, and E3 respectively. The resolution of the inner patch is then defined as NxM where N = max(E0,E2)-2 and M = max(E1,E3)-2. This choice for NxM conservatively rounds up the degree of the inner patch to highest boundary degree both vertically and horizontally. The 4 strips generated are created from boundary edge vertices and the perimeter inner mesh vertices. S0=strip(E0,Nl), S1=strip(E1,Mt), S2=strip(E2,Nr), S3=strip(E3,Mb). See Figure 2.

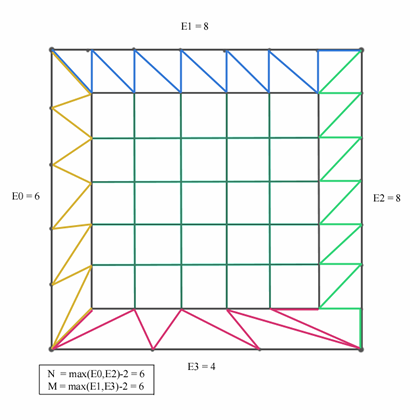Figure 2: Non-uniform mesh evaluation

The LOD heuristic is chosen as a function of distance from the camera position C_pos. A minimum LOD_min and maximum LOD_max boundary evaluation is chosen. A distance from the camera for minimum Dist_near and maximum Dist_far level of detail is chosen. Only the end control points of each edge p₀ and p₁ are used to determine the degree evaluation.

For speed the dist function is actually chosen as the squared distance as apposed to the square root. For a visible distance of 500 meters the near distance would be something like 25 meters and the far lets say 250 meters. All boundary edges at 25 meters or closer will have maximum detail. All boundary edges at 250 meters or farther will be minimum level of detail. If we choose a good distance range relative to average patch edge length and only a few different LOD levels then most patches will be uniformly tessellated with non-uniform patches existing as a row of patches connecting different uniform levels of detail at a fixed radius to the camera.

More exotic heuristics can be chosen that take into account things like edge or patch curvature, however one must be careful to ensure that the heuristic exhibits good hysteresis so that patches do not fluctuate between different LODs giving away the effect.

Conclusions and Future work

The terrain system discussed in this paper has been implemented in SSX, and SSX Tricky. The system stores only patch control information requiring a much smaller memory footprint over vertex geometry. Through dynamic level of detail the number of polygons rendered by the graphics hardware is reduced without noticeable quality loss. The system does not introduce seams between patches of different tessellation levels by ensuring identical edge tessellation on boundaries between patches that maintain C0 continuity. Neighbouring information is not required at run time in order to avoid LOD seems.

For terrain systems that have limited memory storage (especially video game consoles) but still require large environments and high geometric detail, Bézier patches provide very good compression. The cost of rendering terrain geometry at constant resolution is more expensive than necessary and does not scale well to lower powered graphics hardware. The system presented here attempts to decrease the memory and polygon costs of rendering a complex terrain. With the addition of a patch caching system the performance of this terrain architecture would scale nicely across lower powered machines.

For Further Information

Michael E. Mortenson, Geometric Modelling Second edition. Wiley Computer Publishing, 1997

Watt & Watt, Advanced Animation and Rendering Techniques Theory and Practice. Addison-Wesley, ACM Press. 1992

Foley, vanDam, Feiner, and Hughes, Computer Graphics: Principles and Practice. Second Edition. Addison-Wesley Publishing, 1990

Copyright © 2000-2001 CMP Media Inc. All rights reserved.